matplotlib es la biblioteca estándar de Python para generar
gráficas. El nombre de matplotlib viene de la intención original
de emular la apariencia de gráficas generadas con MatLab.
En lugar de un tutorial al uso, aquí me voy centrar en ejemplos concretos de figuras publicadas en algunos de mis papers. Los ejemplos están escogidos de papers que han sido publicado en open access, con lo cual no hay problemas de copyright.
Ejemplo 1: figura sencilla¶
Vamos a empezar con la siguiente figura:
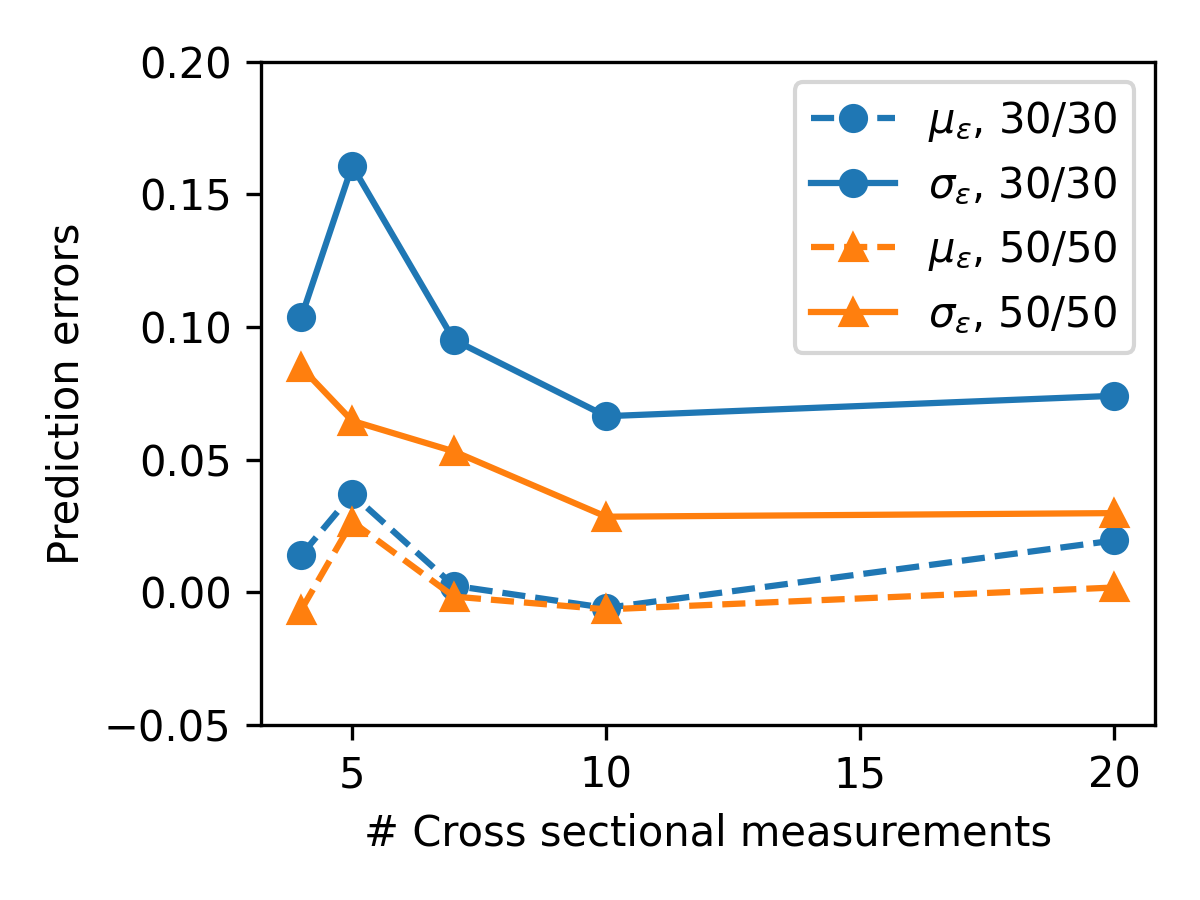
Figure 1:Ejemplo 1 - figura creada en matplotlib
El código que genera esta figura es el siguiente:
import numpy as np
import matplotlib.pyplot as pt
data = np.load("data30.npy")
data2 = np.load("data50.npy")
mlist = data[:,0]
slist = data[:,1]
mlist2 = data2[:,0]
slist2 = data2[:,1]
Npoints = [4, 5, 7, 10, 20]
pt.figure(figsize=(4,3))
pt.plot(Npoints, mlist, 'o', linestyle='--', color="C0", label=r"$\mu_\varepsilon$, 30/30")
pt.plot(Npoints, slist, 'o', linestyle='-', color="C0", label=r"$\sigma_\varepsilon$, 30/30")
pt.plot(Npoints, mlist2, '^', linestyle='--', color="C1", label=r"$\mu_\varepsilon$, 50/50")
pt.plot(Npoints, slist2, '^', linestyle='-', color="C1", label=r"$\sigma_\varepsilon$, 50/50")
pt.legend()
pt.ylim(-0.05,0.20)
pt.xlabel("# Cross sectional measurements")
pt.ylabel(r"Prediction errors")
pt.tight_layout()
pt.savefig("profiles_number.png", dpi=300)
pt.show()Hagamos un análisis línea a línea del código.
Importar la librería¶
El script comienza con las líneas:
import numpy as np
import matplotlib.pyplot as ptÉsta es la forma estándar de importar módulos en Python. En concreto,
estamos importando dos módulos: el módulo pyplot dentro de matplotlib y la librería numpy, que es un paquete para trabajar con vectores, matrices y arrays multidimensionales.
Para hacernos la vida más fácil, en lugar de tener que usar pyplot y numpy usamos as pt y as np para asignar nombres más cortos.
Importar los datos¶
Las líneas:
data = np.load("data30.npy")
data2 = np.load("data50.npy")
mlist = data[:,0]
slist = data[:,1]
mlist2 = data2[:,0]
slist2 = data2[:,1]
Npoints = [4, 5, 7, 10, 20]importan los datos que vamos a representar en la figura. data y data2 son dos
arrays bidimensionales que se leen de dos ficheros usando la función load de numpy.
La instrucción:
mlist = data[:,0]selecciona todos los datos de la primera columna (en Python se empieza a contar desde zero) y los guarda en un vector.
Crear una figura¶
La línea:
pt.figure(figsize=(4,3))crea una figura en matplotlib. Una cosa que puede parecer sorprendente
es que no tenemos necesariamente que asignar la figura a una variable. La figura que hemos creado se convierte en la figura activa por defecto.
figsize es un argumento que nos permite definir el tamaño de la figura, en este caso en pulgadas (2.5 cm, aproximadamente). La figura
tiene por tanto unas dimensiones de 4 pulgadas en horizontal y 3 en vertical. El motivo para usar 4 pulgadas es que los papers suelen publicarse a dos columnas, y el ancho de una página letter o A4 es del orden de 20cm.
Representar los datos¶
Las líneas:
pt.plot(Npoints, mlist, 'o', linestyle='--', color="C0", label=r"$\mu_\varepsilon$, 30/30")
pt.plot(Npoints, slist, 'o', linestyle='-', color="C0", label=r"$\sigma_\varepsilon$, 30/30")
pt.plot(Npoints, mlist2, '^', linestyle='--', color="C1", label=r"$\mu_\varepsilon$, 50/50")
pt.plot(Npoints, slist2, '^', linestyle='-', color="C1", label=r"$\sigma_\varepsilon$, 50/50")definen cuatro gráficas usando la función plot. Los dos primeros argumentos, por
ejemplo Npoints y mlist representan las coordenadas en el eje X y en el eje Y. Como
hemos visto antes, son listas o vectores unidimensionales. El tercer argumento 'o' o '^'
especifica que queremos usar círculos y triángulos para representar los datos.
Después de estos tres argumentos, vienen una serie de opciones:
linestyle='--'especifica que queremos unir los puntos con una línea discontinua.color="C0"especifica que queremos que los puntos y las líneas tengan el primer color de la paleta de colores (en este caso el estilo por defecto).matplotlibdefine por defecto una paleta de colores para que las gráficas que se representan en los mismos ejes puedan diferenciarse.label=r"$\mu_\varepsilon$, 50/50"especifica el texto para la leyenda de la figura.matplotlibpermite usar LaTeX, en este caso el texto contenido entre los dos signos de dólar$. Para evitar que Python interprete los caracteres detrás de la barra invertida\, añadimos unarantes de la cadena de texto (rde raw)
Definir los ejes y la leyenda¶
Las líneas:
pt.legend()
pt.ylim(-0.05,0.20)
pt.xlabel("# Cross sectional measurements")
pt.ylabel(r"Prediction errors")nos permiten añadir información a la figura.
pt.legend()le indica amatplotlibque queremos incluir una leyenda. Al no pasarle ningún argumento,matplotlibintenta colocarla en la posición que moleste menos.pt.ylim(-0.05, 0.20)nos permite especificar los límites del eje Y.pt.xlabelypt.ylabeldefinen los títulos de los ejes, usando la fuente y tamaño por defecto.
Optimizar las dimensiones, guardar y mostrar la figura¶
pt.tight_layout()
pt.savefig("profiles_number.png", dpi=300)
pt.show()tight_layout se encarga de optimizar las dimensiones de la figura, mientras que
savefig es el comando que permite guardar la figura como una imagen. En este
caso, hemos escogido el formato png con una resolución de 300 puntos por pulgada.
Finalmente, show hace que aparezca una ventana donde se muestra la figura. De esta
manera, es posible iterar la figura hasta conseguir el formato deseado.
Ejemplo 2: figura múltiple¶
En papers es muy común tener figuras con varias partes. Por ejemplo:
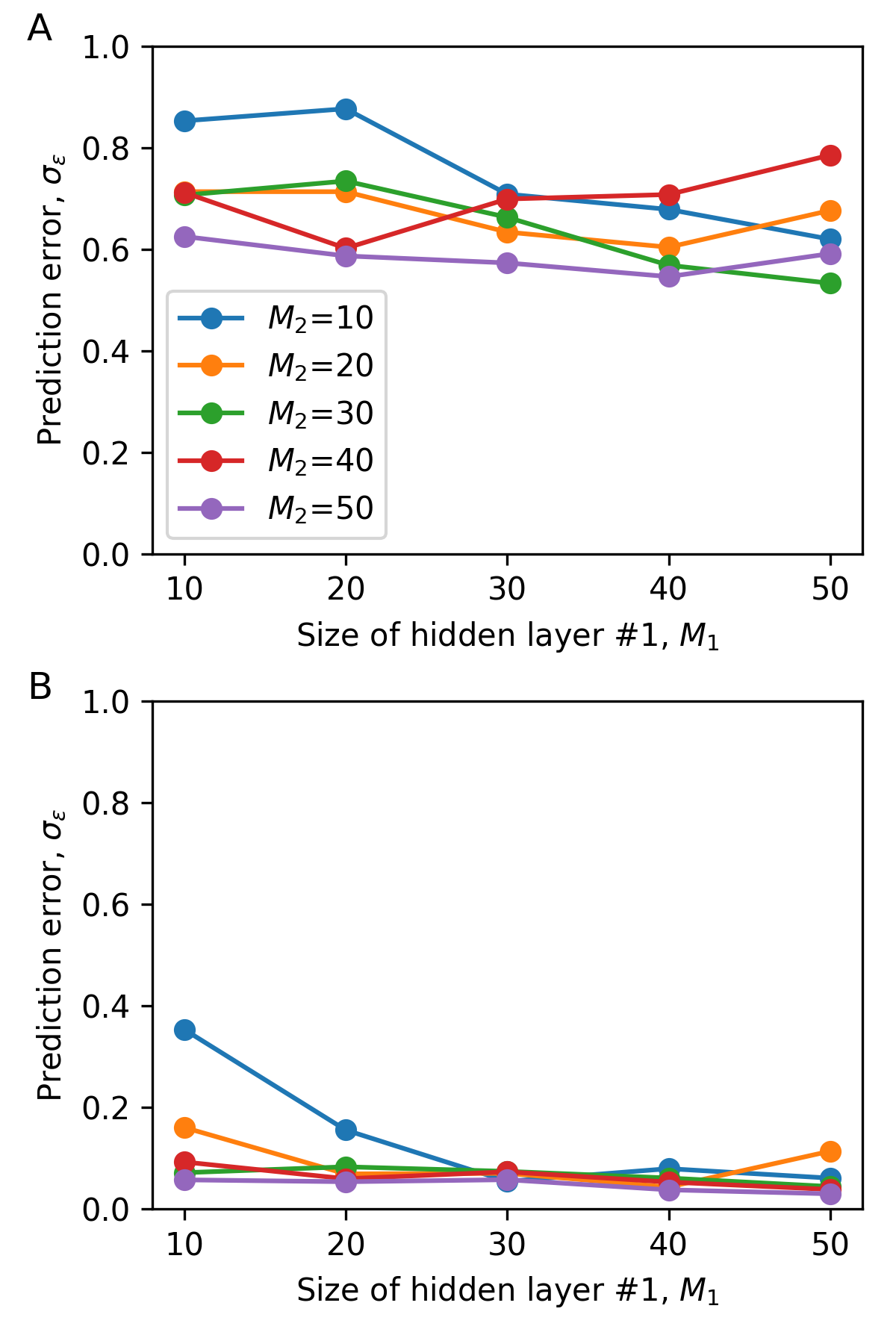
Figure 2:Ejemplo 2 - figura múltiple creada en matplotlib
En esta sección me voy a centrar
en cómo crear figuras múltiples usando matplotlib.
Empecemos con el código que genera esta figura:
import numpy as np
import matplotlib.pyplot as pt
pt.figure(figsize=(4,6))
pt.subplot(211)
seps = np.load("./results/resultsA.npy")
labels = [10,20,30,40,50]
for j in range(5):
pt.plot(labels, seps[j,:], 'o', linestyle="-", label="$M_2$={}".format(labels[j]))
pt.ylim(0,1.0)
pt.legend(loc="lower left")
pt.xlabel("Size of hidden layer #1, $M_1$")
pt.ylabel(r"Prediction error, $\sigma_\varepsilon$")
pt.subplot(212)
seps = np.load("./results/resultsB.npy")
labels = [10,20,30,40,50]
for j in range(5):
pt.plot(labels, seps[j,:], 'o', linestyle="-", label="$M_2$={}".format(labels[j]))
pt.ylim(0,1.0)
pt.xlabel("Size of hidden layer #1, $M_1$")
pt.ylabel(r"Prediction error, $\sigma_\varepsilon$")
pt.tight_layout()
pt.figtext(0.03,0.97,"A",fontsize=12)
pt.figtext(0.03,0.48,"B", fontsize=12)
pt.savefig("stdev_error.png", dpi=300)
pt.show()El comienzo¶
El código comienza de manera muy parecida al ejemplo anterior:
import numpy as np
import matplotlib.pyplot as pt
pt.figure(figsize=(4,6))La diferencia es que ahora la figura mide 4 pulgadas de ancho y 6 de altura, es decir, es el doble de alta para acomodar los dos ejes.
Crear múltiples ejes en una figura¶
La clave para definir múltiples ejes es la línea:
pt.subplot(211)Esta instrucción le dice a matplotlib que queremos generar una figura con múltiples
ejes, y que el siguiente eje es el primer eje de una matriz 2x1, donde 2 representa
el número de filas y 1 el número de columnas. De ahí que el argumento de subplot
sea 211.
Contenido del primer eje¶
Al igual que en el ejemplo anterior, usamos numpy para copiar los datos de un
fichero en un array bidimensional. La diferencia es que en lugar de usar llamadas
a plot individuales para representar los datos, aquí usamos un bucle for:
for j in range(5):
pt.plot(labels, seps[j,:], 'o', linestyle="-", label="$M_2$={}".format(labels[j]))La interpretación es la siguiente: para cada j entre 0 y 5, vamos a representar
la fila j de nuestro array bidimensional seps, usando círculos unidos por líneas.
El texto de la leyenda la especifica el argumento:
label="$M_2$={}".format(labels[j])En este argumento asignamos a label una cadena de texto donde para cada j estamos
incluyendo el valor contenido en el elemento j de la lista labels definida en la línea nueve. Para ello hacemos uso del método format, el cual sustituye {} por el valor o valores que pasamos como argumento.
Estas dos líneas representan un ejemplo de cómo integrar aspectos de programación en
la creación de figuras. Hasta ahora, el ejemplo anterior contenía simplemente una
lista de instrucciones. Aquí hacemos uso de dos construcciones de Python, el bucle
for y las herramientas para hacer sustituciones en cadenas de texto, para
simplificarnos la vida y evitar tener que escribir a mano cada una de las gráficas de
los ejes.
Definición del segundo eje¶
Nos saltamos unas cuantas líneas para llegar a la definición del segundo eje de la figura:
pt.subplot(212)Como mencionamos antes, tenemos una matriz 2x1 y este eje corresponde al elemento 2, que en este caso ocupa la segunda fila.
Contenido del segundo eje¶
El contenido del segundo eje se define igual que el primero. Simplemente destacar
que estamos reusando el nombre seps para definir los datos contenidos en
un fichero distinto. Redefinir seps no cambia el contenido del eje de arriba.
Ajustar las dimensiones¶
La función:
pt.tight_layout()se encarga de ajustar las dos figuras al tamaño de la figura. En el caso de figuras múltiples esto es importante para evitar que los ejes y los títulos se pisen los unos a otros o se salgan fuera de los límites de la figura
Añadir los identificadores de los ejes¶
Finalmente, tenemos que identificar el eje superior como la figura A y el de abajo como la figura B. Esto se hace con los siguientes comandos:
pt.figtext(0.03,0.97,"A",fontsize=12)
pt.figtext(0.03,0.48,"B", fontsize=12)figtext añade un texto en la posición especificada por los dos primeros argumentos.
El primer argumento corresponde a la coordenada horizontal y el segundo a la vertical.
Las dos coordenads están normalizadas entre 0 y 1, de manera que (0,0) corresponde
a la esquina inferior izquierda, y (1,1) a la superior derecha. El argumento fontsize
determina el tamaño de la fuente, en este case 12 puntos.
Un poco de historia¶
Matplotlib fue creado John D. Hunter, motivado por la necesidad de encontrar una forma sencilla y flexible de representar electroencefalogramas durante su investigación postdoctoral. Hunter comenzó a trabajar en lo que se convertiría en Matplotlib en 2003, y pronto empezó a recibir contribuciones de múltiples usuarios interesados en desarrollar la librería. Tras su fallecimiento en 2012, el copyright pasa al Matplotlib development team liderado por Michael Droettboom.
El uso de Matplotlib está muy extendido en la comunidad científica, hasta el punto que la NASA ha creado una beca para promover su desarrollo. Matplotlib es la herramienta que se usó para crear la primera imagen de un agujero negro y ha contribuido a la visualización y representación de datos en miles de artículos. John D. Hunter recibió de manera póstuma el primer Distinguished Service Award otorgado por la Python Software Foundation.